|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
Navigation
by Lunar Distance
Please be patient, 590 kB of Java code
to be loaded ...
|
|
Enter latitude in decimal degrees and press return key, |
|
|
you may use the keys "h", "d", "m", "n" to increase the
hour, date, month, or minute, |
 |
For the
"Horizon Rectang." view and the "Horizon Spher." view
the apparent lunar distance of the Sun, Venus, Mars,
Jupiter, and Saturn will be displaid selecting from
the "Details" menu. Details for clearing the lunar distance are found in the data windows from the corresponding itemd of the"Write/Draw" menu. |
| The lunar distance is
the angle between the Moon and the Sun or a celestial
body (planet, star). By this method the Greenwich time
can by calculated, using an almanach with the tabulated
values. Then the longitude can be determined without a
chronometer. Lunar Distances were used to determine longitude at sea in the period from about 1770 (Lunar Tables by Tobias Mayer) until 1850, but rarely after that date. This was a time when chronometers were not yet widely available at a reasonable price and were considered unreliable on long voyages. But the lunars tables were not dropped from the US "American Ephemeris & Nautical Almanac" until 1912, from the German "Nautisches Jahrbuch - Ephemeriden und Tafeln" as late as 1924. Captain Joshua Slocum (1844-1909), the first man to sail single-handedly around the world, wrote in Sailing Alone Around the World (1900 first edition) Chapter XI: >>On the forty-third day from land, - a long time to be at sea alone - the sky being beautifully clear and the moon being "in distance" with the sun, I threw up my sextant for sights. I found from the result of three observations, after long wrestling with lunar tables, that her longitude by observation agreed within five miles of that by dead-reckoning. This was wonderful; both, however, might be in error, but somehow I felt confident that both were nearly true, and that in a few hours more I should see land; and so it happened, for then I made the island of Nukahiva, the southernmost of the Marquesas group, clear-cut and lofty. The verified longitude when abreast was somewhere between the two reckonings; this was extraordinary. All navigators will tell you that from one day to another a ship may lose or gain more than five miles in her sailing-account, and again, in the matter of lunars, even expert lunarians are considered as doing clever work when they average within eight miles of the truth.<< Using a sextant, the navigator precisely measures the angle D' between the limb of the Moon and the Sun. 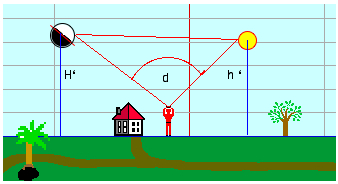 First correction: The first correction to the observed lunar distance d is the distance between the limb of the Moon (rM) and its center and the limb of the Sun and its center (rS): 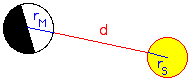 D' = d + rM + rS Second correction: The almanac gives geocentric lunar distances (as they would appear from the center of the Earth). Therefore the lunar distance has to be corrected for the effects of atmospheric refraction (R) and parallax (P). 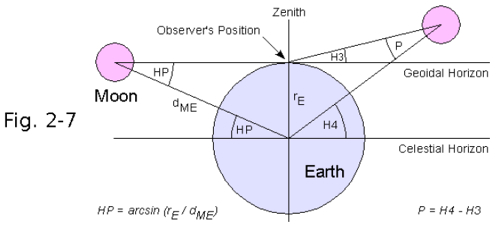 The topocentric apparent altitude of the Moon H3=H' has to be converted to the geocentric altitude H4=H taking into account refraction (R) and parallax (P). The equatoreal horizontal parallax is HP = arcsin(rE/dME), and the parallax P = arcsin[sin(HP)*cos(H' ). H = H'
- R + P = H'
- R + arcsin[sin(HP)*cos(H'
)]
The geocentric altitude h of the Sun is obtained from the topocentric apparent altitude h': h = h'
- r + p = h'
- r + arcsin[sin(rE/dSE)*cos(h'
)]
Clearing the lunar distance: By Dunthorne's formula the geocentric lunar distance D can be computed from D: 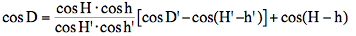 The unknown
time TD corresponding with D is found by
(linear) interpolation from the tabulated lunar
distances D1 and D2 at the
times T1 and T2
(D between D1 and D2):
TD
= T1 + (T2-T1)*(D-D1)/(D2-D1)
Accuracy: An error of only 1' in the measurement of D' is an error of approximately 2 minutes in time or 0.5° in longitude or 40 km in position at mid latitudes. Simulated Example:
The geocentric lunar distance D at the time T is computed from the geocentric ecliptical longitudes (L1, L2) and latitudes (B1, B2) by the Planets applet (accuracy 2'', comparision with the precise results of MICA, Multiyear Interactive Computer Almanac, U.S. Naval Observatory): 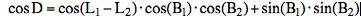 Berlin, 52.51°N, 13.41°E, on 2010 Feb 24 at 14:00 UT: 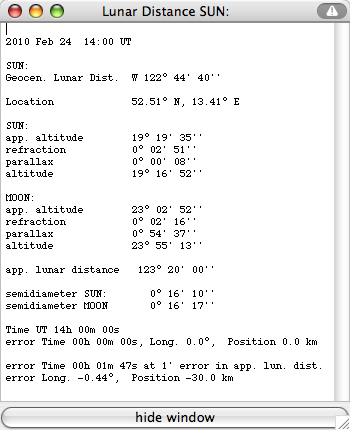 The apparent altitudes of the Sun and the Moon (h', H') are also computed by the Planets applet, as well as the geocentric altitudes (h, H) taking into accout refraction and parallax and the apparent lunar distance D' (using Dunthorne's formula resolved for D'). Of course the time computed from D, D1 and D2 will agree with T. Assuming an error of only 1' for the apparent lunar distance D' the time error will be about 2 minutes, and the error in geographic longitude about 0.5° or 40 km in position at mid latitudes. Additional errors of a few arcminutes in the altitudes h, h', H, H' don't increase very much the errors of longitude. More corrections due to refraction (temperature, pressure, flatening of the lunar/solar disk) and to the ellipsoidal flattening of the earth have to be taken into account for precise results. |
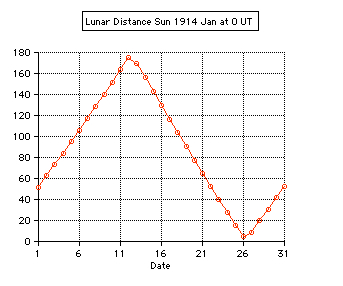
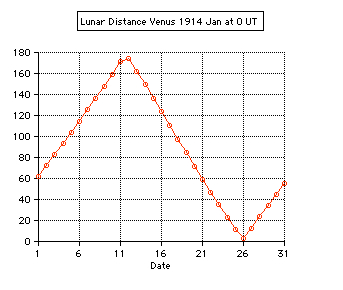
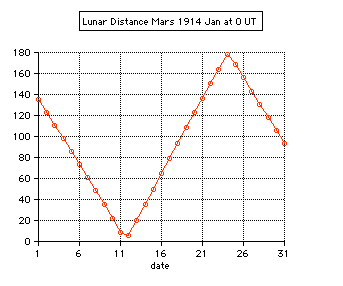 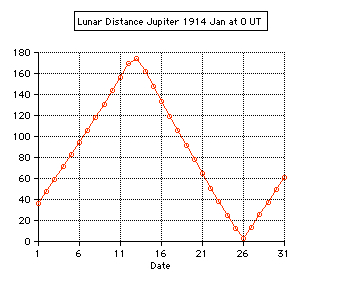
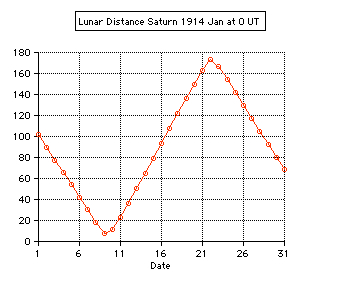 Tests: - Total solar eclipse of 1999 Aug 11 in Karsruhe (Germany) 49.005° N, 8.386° E: The apparent lunar distance of the Sun is computed 0° 00' 00'' from 10:29 until 10:38 UT, semidiameter Sun 15' 47'', Moon 16' 01''. - Total solar eclipse of 2006 Mar 29 in Side (Turkey) 36.767° N, 31.367° E: The minimum apparent lunar distance of the Sun is computed 0° 02' 32'' at 10:56 UT, semidiameter Sun 16' 01'', Moon 16' 35''. The numerical algorithms of the applet are using the Ephemeris Time scale (ET, now continued by the Terrestrial Time TT). Thefore the difference ∆T = ET - UT is needed using UT. The values of ∆T are estimated after 2010. 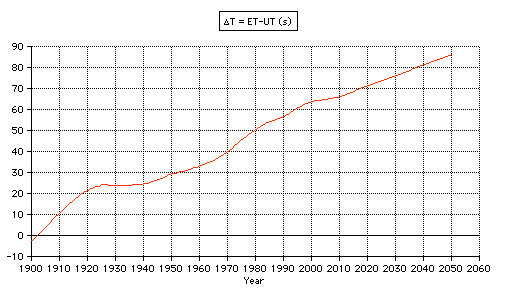 |
The features of the Planet Applet are described here
Updated:
2023, Oct 04
©
2010-2023 J. Giesen
![]()


