Brachistochrone: Path of Shortest Time (applet)

Brachistochrone

	Select the run mode. You can add and compare an inclined plane, a root curve, or a free fall.
	Select the difference ∆H between start point A and end point B on the brachistochrone.
	Select the number of steps. The precision is of course depending on the step size.
	The button draws diagrams v(t), and v(x).

A point-like body that starts at the first point A with zero speed and is constrained to move along the curve to the second point B (B lower than A, constant gravity g, no friction).

The curve that is covered in the least time is a brachistochrone curve. It is an upside down cycloid passing vertically through A and B.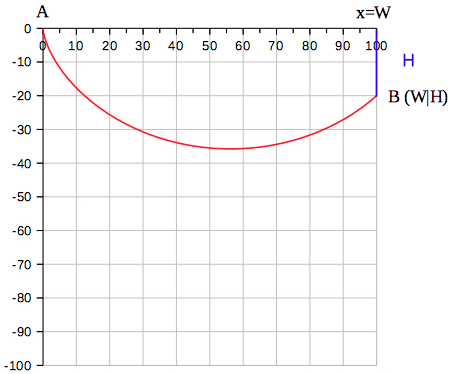

The cycloid through the origin A, with a horizontal base given by the line y = 0 (x-axis), generated by a circle of radius R rolling over the "positive" side of the base (y ≥ 0), consists of the points (x, y), with

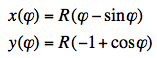where φ is a parameter, corresponding to the angle through which the rolling circle has rotated.

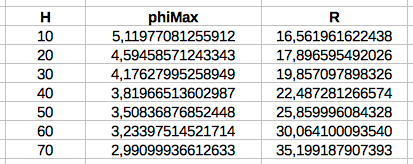
Fitting the maximum angle φ_m and the radius R and to reach point B(100m, H) WolframAlpha was used solving the equation: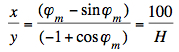

⁽¹⁾

Then the radius R can be calculated by:

⁽²⁾

^{For steps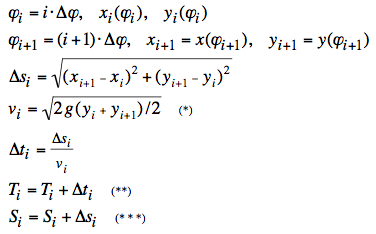} the following calculations are performed (i=0 .. i<N):

(*) applies because of the energy law. T_N (**) is the total travel time from A to B, and S_N (***) the total arc length along the cycloid from A to B.
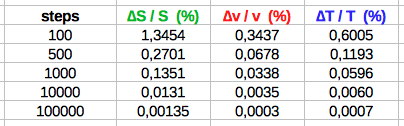
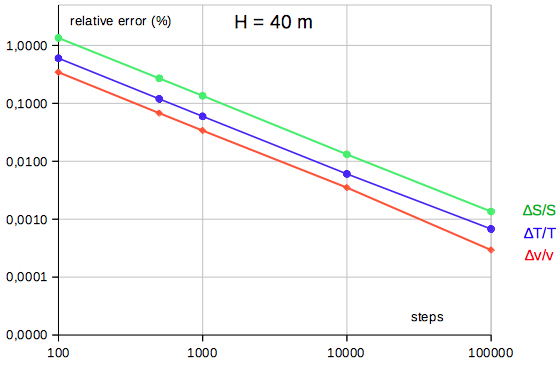
The final velocity at B is:

⁽³⁾

Furthermore the theoretical arc length is:

⁽⁴⁾

and the theoretical total travel time (#):

⁽⁵⁾

The precision of the results for v, S, and T by the formulas (3), (4), and (5) - compared with (*), (**), and (***) - is of course depending on the number of steps:

From (1), (2), and (5) we get: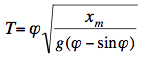

T(φ) has a minimum of T=5.659 s at φ = π, using x_m=100 m, g=9.81 m/s^2: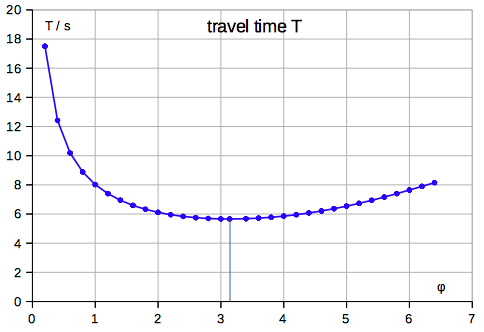

The minimum of travel time occurs at H=200m/pi = 63,66 m: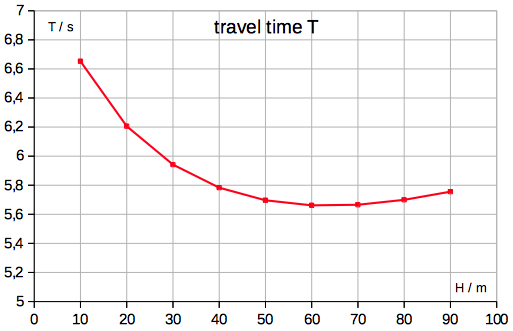

Example of results along the brachistochone (∆H=30m, n=100,00 steps):

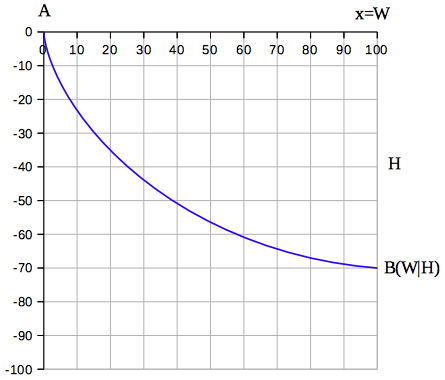
t = 5.94177 s is the numerical traval time, T = 5.9417 s the theoretical result by formula (5),
s = 118.7115 m is the numerical arc length, S = 118.7115 m the theoretical result by formula (4).

You can add a root curve and compare it with the brachistochrone:

The arc length of the root curve

can be computed by the formula by (##):

Tautochrone

A tautochrone or isochrone curve is the curve for which the time taken by an object sliding without friction in uniform gravity to its lowest point B is independent of its starting point A.
The curve is also a cycloid.

The coordinates of point B are x=R·π and y=2R

The time of descent is:

^(#)