Quadratum Horarium Generale (Regiomontanus
Dial)
Uhrentäfelchen
| This instrument
is a portable sundial for all latitudes, developed by
Regiomontanus (1436-1476). It also indicates the time
of sunrise and sunset. It is equipped with a simple Sun sight on the upper edge. A thread with a sliding bead is hanging from the point of suspension (at the end of a brachiolus) which is adjustable in two dimensions (declination, latitude). |
See
instructions for interactive use below
Capuchin Dial (single
latitude)
 |
Enter
the year
into text field and hit "Apply input". (Gregorian Calendar only, later than 1582) |
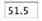 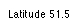 |
Enter
the latitude
(decimal degrees) into the text field and hit "Apply
input". The latitude is indicated in the text field. |
 |
The
interactive regions (light gray scales) are changing
the cursor to cross hair. |
 |
Click into the
degree scale (light gray) on the lower and left limb to
direct the quadrant to the Sun. The thread will follow
the elevation angle. |
 |
Use the "Today"
button to set the thread to the current date. The bead
is set to the current Sun's declination. |
 |
- Click into
the light gray calendar (date scale,
upper part for winter and
spring, or lower part for summer and autumn) to set
the thread to the date. - To bead is set to the declination (by the declination scale at right) automatically. |
 |
Read
the date, the declination, and the time of sunrise and
sunset (neglecting refraction on the horizon), the
equation of time, the current time, and elevation as
computed by astronomical algorithms. |
| Select
from the "Display Options" menu. |
|
| The
red frame of the applet area is a square (753 x 753
pix, same size as for Gunter's quadrant). |
|
| The dial is
obeying the equation of the nautic spherical triangle
(h = elevation angle,
φ = latitude, AH =
hour angle):
sin h = sin φ sin δ + cos φ cos δ cos AH
Spherical triangles are the subject of the 4th and 5the book "De Triangulis" by Regiomontanus. The formula is symmetric with respect to φ and δ, thus the dials of Regiomontanus and Apian are equivalent. A very short proof (by E. Guyot) can be found in the book of Rohr: 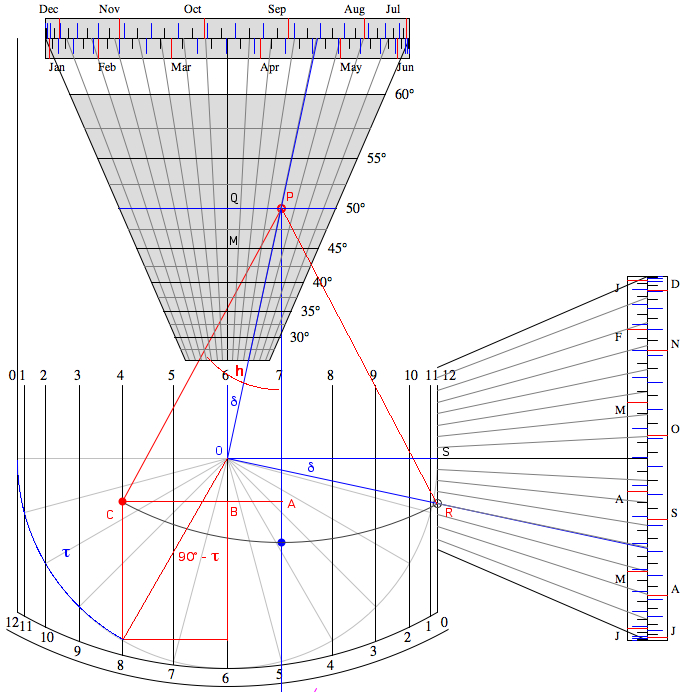 φ = Latitude, h = Altitude, δ = Declination, τ = Local Hour Angle The thread is suspended at P and the bead is set to R. The radius r = MO = OS = 1 is set to unity. OQ = tan φ SR = tan δ PQ = tan φ tan δ The angles POQ and ROS are equal to the declination δ. The triangle ∆POR is rectangular: PR2 = OR2 + OP2 = OS2 + SR2 + OQ2 + PQ2 = 1 + tan2 δ + tan2 φ + tan2 φ tan2 δ PR2 = (1 + tan2 φ) (1 + tan2 δ) = 1 / (cos2 φ cos2 δ) PR = 1 / (cos φ cos δ) Directing the dial to the Sun the bead is at C and the altitude angle is h. The hour angle is τ and BC = sin (90°-τ) = cos τ AC = PR sin h = sin h / (cos φ cos δ) = AB + BC = tan φ tan δ + cos τ sin h / (cos φ cos δ) = tan φ tan δ + cos τ sin h = sin φ sin δ + cos φ cos δ
cos
τ
|

Regiomontanus
monument in Königsberg (Bavaria)


Regiomontanus'
birthplace in Königsberg
| Books |
| Rohr,
René R. J.: Die
Sonnenuhr. Geschichte, Theorie, Funktion. Callwey, München 1982. Meyer, Jörg: Die Sonnenuhr und ihre Theorie. Harry Deutsch, Frankfurt 2008. |
|
|
|
Regiomontanus:
De
Triangulis
Planis
Et
Sphaericis
Libri
Cinque
(1561)
Regiomontanus, Apian and Capuchin
Sundials Das
Allgemeine Uhrentäfelchen von Regiomontan Tragbare Sonnenuhren in Europa ab 1400
(PDF) Uhrentäfelchen von P. Aegid Everard Pourquoi le cadran de Regiompntanus
fonctionne-t-il ? Les cadrans de hauteur à lignes horaires rectilignes
Horoscopion Apiani Generale Dignoscendis
Horis cuiuscumque generis aptissimum Quadratum Horarium Generale Georgius
Hartman Quadratum horarium generale (1496) |
©
2009-2023 J. Giesen
