Sieve for Prime Numbers by a Rectangular Hyperbola
| The page "Crible
géométrique (hyperbole)" by Jean-Paul Davalaninspired
me to write the interactive Java applet below. On the rectangular hyperbola y = k/x (k>0, x natural number) mark two points P1(x1 , y1) and P2(x2 , y2), and draw the secant through P1 and P2. In case of x1 = x2 = x draw the tangent of the hyperbola y = - k/x2 + 2k/x. Then from (-k, 0) draw a second line perpendicular to the first, which will intersect the y-axis at (0, x1 · x2). The points of intersection are (0, x1 · y1) indicate the product, omitting the prime numbers {2, 3, 5, 7, 11, 13, 17, 19, 23,
29, 31, 37, 41, 43, 47, ...}
if x1≠1
or x2≠1.
The construction also interprets the multiplication of real numbers. |
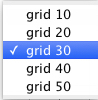 |
Select the grid size (pixels). |
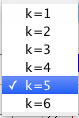 |
Select the the constant k of the
parabola y=k/x. |
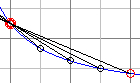
| Click two integers on the horizontal axis,
the cursor will change to cross hair. The first click is marked by a fat circle. |
|
  |
Hold down the command key to add
subsequent clicks. |
| If two points are marked the menu will
be enabled. |
|
 |
Selecting "2 lines" will add the
points at x1+1, x1+2 selecting "3 lines" will add the points at x1+1, x1+2, x1+3 and so on. |
The slope m of the first line
through P1 and P2
is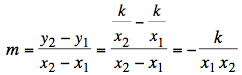 and the slope of the perpendicalar line
The equation of this line,
intersecting the vertical axis at y(0) = x1
·
x1
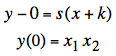 The first line (secant or
tangent) intersects the vertical axis at (0,
k[1/x1
+ 1/x2])
For the point of intersection of the two lines (xs, ys) we find: 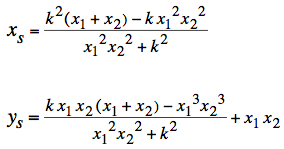 |
|
|
Crible géométrique (hyperbole) (Jean-Paul Davalan) A Parabola Sieve for Prime Numbers (Wolfram) Catching primes (Abigail Kirk) |
2017-2023 J. Giesen
updated: 20.10.2023