The Rainbow
|
Details:
angular distribution of deflected rays incident angle and deflection angle visibility of rainbows intensity of primary and secondary rainbow estimating the rainbow angle refractive index of water history mathematics of rainbows glass ball experiment The applet is simulating a rainbow and based on geometrical optics only, using Snell's law of refraction, named after Dutch astronomer Willebrord Snellius (1580–1626): 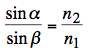 with angles α (incident) and β
(refracted) measured from the normal of the boundary,
and
with the refractive index n of the respective medium. For air, 10 °C, pressure 100 kPa, 100% humidity, 520 nm, (o): n = 1.000283
For water the following values are used (**):In a primary rainbow, the arc shows red on the outer part and violet on the inner side. This rainbow is caused by light being refracted when entering a droplet of water, then reflected once inside on the back of the droplet and refracted again when leaving it. In a double rainbow two inner reflections occur, and a second arc is seen outside the primary arc, and has the order of its colours reversed, with red on the inner side of the arc. The Rainbow Applet is using Snell's law of refraction and the law of reflexion only. The impact parameter of minimum/maxium deflexion was computed using 5000 rays. Applet Results Primary Rainbow:
width of rainbow: 2.02°
Applet Results Secondary
rainbow:
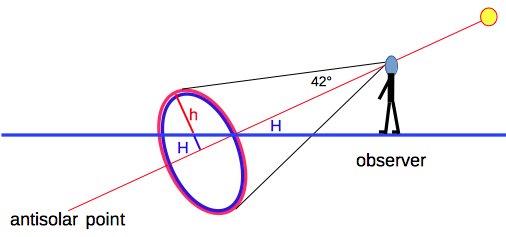
For impact parameters b/R smaller than at extremal deflection the rays extended backwards are convergent (gray), otherwise they are divergent (check the box "Extend").  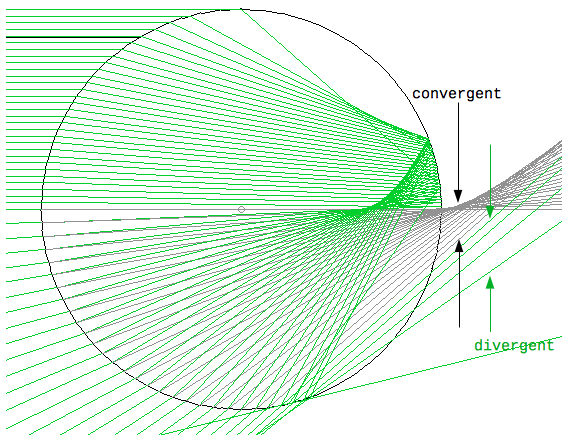 The cone of rainbow is centered on the line to the antisolar point, opposite the Sun from the viewpoint of an observer. The primary rainbow is visible only when the altitude H of the sun is less than 42°. :
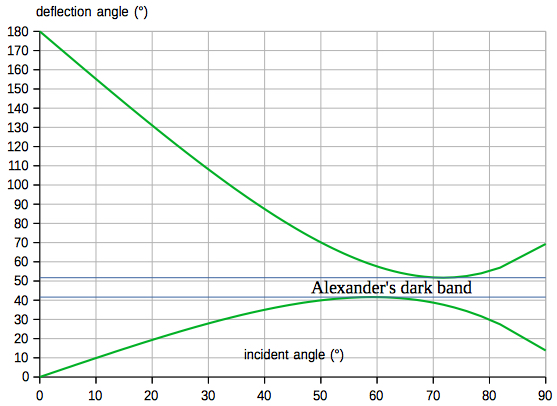
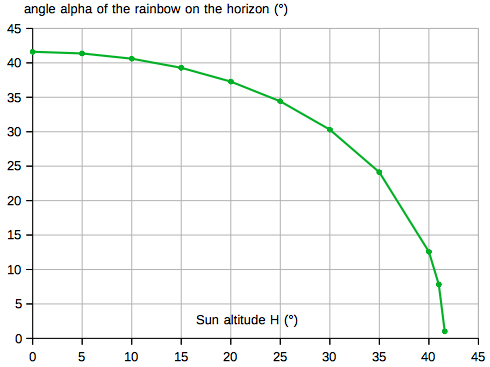
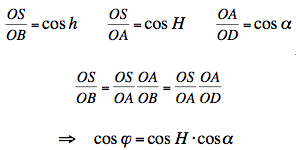 The angle α as a function of the
Sun's altitude H is shown in the following
diagram:
 Angular distribution
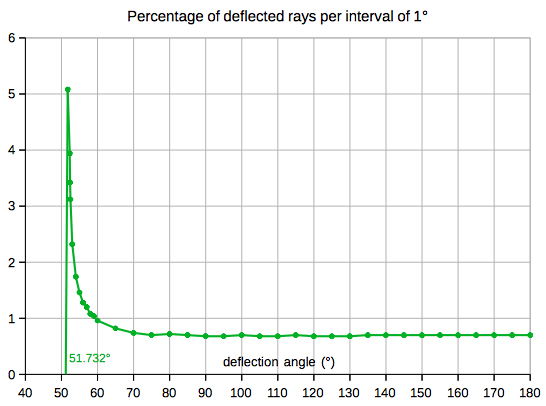
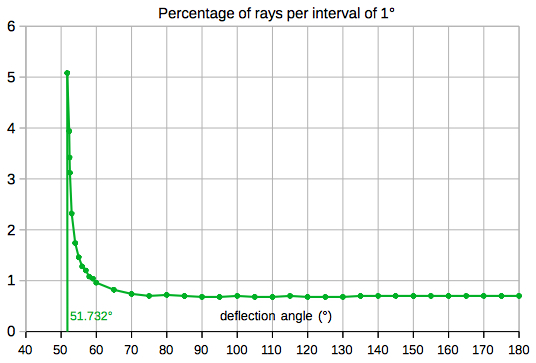
For the primary rainbow, using 5000 rays, they are
distributed like this. The rays are concentrated at
the extreme angle of deflection (41.61°, or 138.39°,
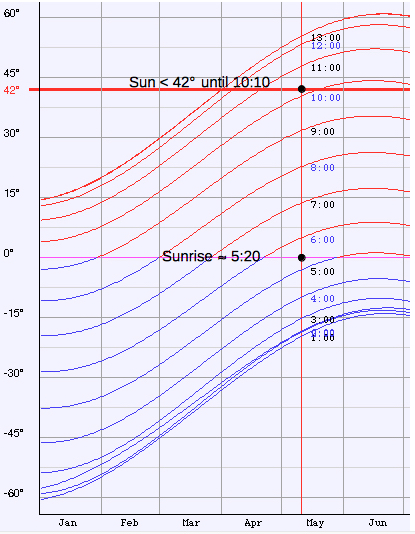
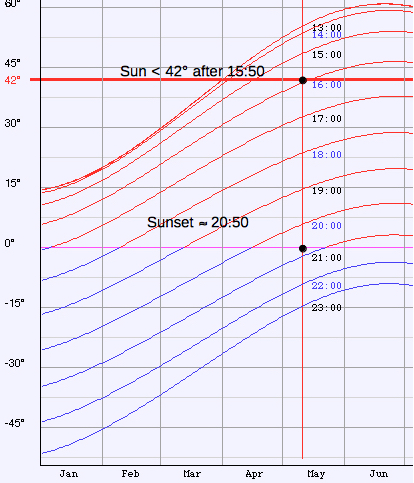
for green):The interval of time for observation, if any, can be evaluated for any location and date of the year by my Azimuth and Elevation Applet, eg. Berlin (52.51° N, 13.41° E): 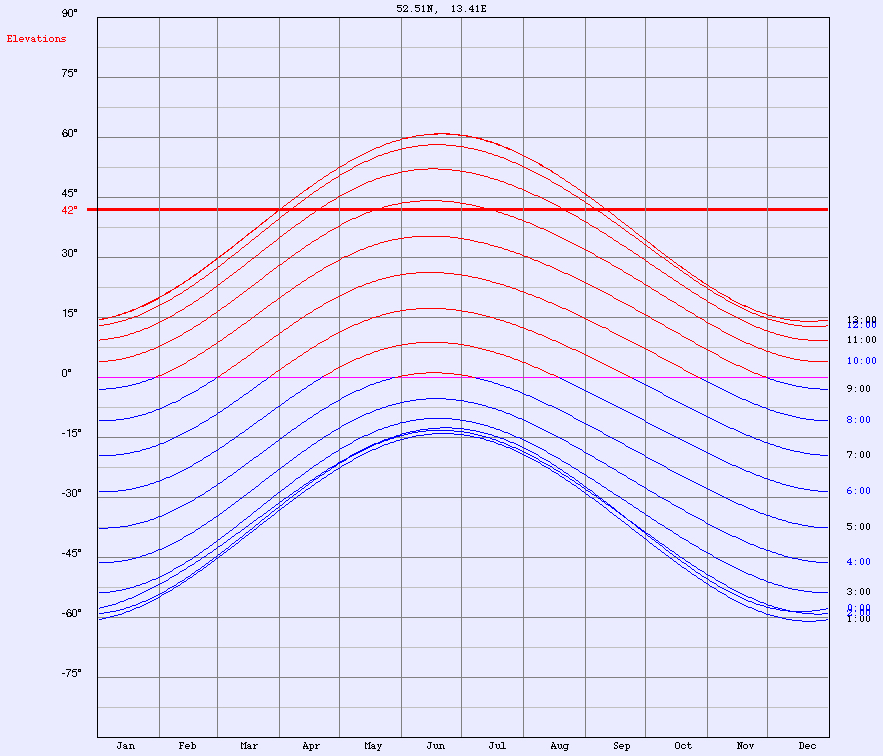 Select "Elevation/AM" or "Elevation/PM" from the menu: e. g. on May 10, the altitude of the Sun is less than 42° from sunrise to about 10:10 and from about 15:50 to sunset (local time CEST) :
The intensity ratio of primary and secondary rainbow can be calculated using the interval of the impact parameter b/R for angles ±1° below or above the the minimum or maximum deflexion angle: 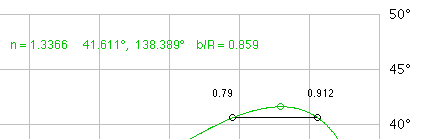 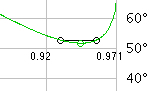 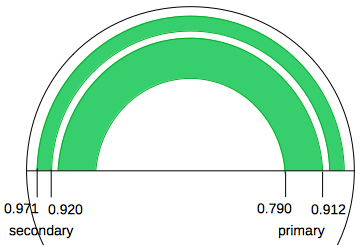 The intensity ratio secondary/primary can by aproximated by the areas of the arcs (0.9712 - 0.9202)/(0.9122
- 0.7902) = 0.0964/0.208 = 0.464
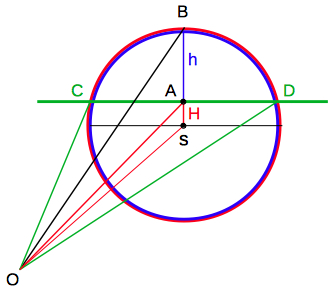
For the primary rainbow the rainbow angle can be calculated: 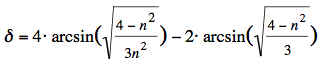 At extreme deflection (primary and secondary rainbow) the incident angles α and relative impact parameters are: 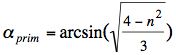
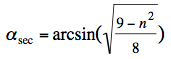 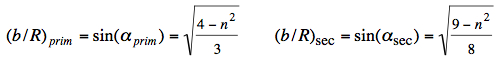 The equations above are
deduced here:
The Mathematics of the Rainbow My rainbow experiment using a
Glass
Ball
Estimating the rainbow angle 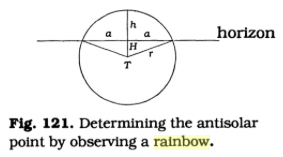 M. Minnaert (Google Books) In his book, Minnaert presents
three equations to estimate the rainbow angle:
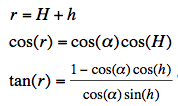 The first equation is obvious, the second can be derived easily. In the 1993 edition of his book, and in the German edition, the third equation has a printing error: tan(r)=1 - [1-cos(α)cos(h)]/[cos(α)cos(h)] is wrong. Refractive index of water: 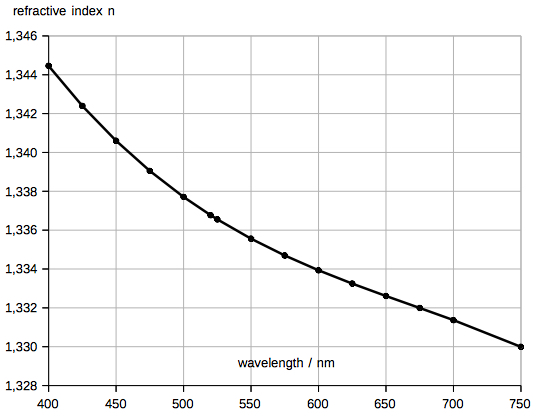 Refractive index of water, based on a table (*) and approximated by a 3rd order polynom. The refractive indices used in my applet (at 400 520, 750 nm) were computed by the formula in (**) for 10° C, mass desity of water 0.999702 g/cm^3 (***) History
Snell's law (1621) was a precondition for a quantitative theory. René Descartes was responsible for the first detailed study of the rainbow in Europe. He showed by using geometric construction and the law of refraction that the angular radius of a rainbow is 42 degrees ("Dioptrics", 1637). Isaac Newton discovered by his experiences with prisms that white light was composed of the light of all the colours of the rainbow ("Opticks", 1704). The wave theory of light was established by Thomas Young (1773-1829) by his interference experiments. George Biddell Airy applied the wave theory, taking into account interference and diffraction ("On the intensity of light in the neighbourhood of a caustic", 1838). He showed that the intensity of light in a rainbow could be modelled using a cubic wave-front and calculated a table of intensity values by his "Airy Integral". Gustav Mie worked on the scattering of an electromagnetic wave by a homogeneous dielectric sphere applying Maxwell's equations ("Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen", 1908). |
|
|
| Refractive
Index of Air Calculator (NIST) (*) The Mathematics of Rainbows (American Mathematical Society) AirySim Mie theory, Airy theory, and the natural rainbow (Raymond L. Lee, Jr.) Refractive index of water Optical properties of water and ice (Wikipedia) (***) Water Density Calculator (Frostburg State University) Light dispersion (Universitat de Barcelona) Regenbogen (Peter Heiß) The Calculus of Rainbows (James Stewart) The Calculus of Rainbows (Jesse Amundsen) Airy theory and rainbows (Philip Laven) |
| Books |
| Minnaert, Marcel: The Nature of Light and
Colour in the Open Air; Dover Pubn Inc; revised ed. 1973;
ISBN 978-0486201962. Minnaert, Marcel: Light and Color in the Outdoors; Springer; 1st ed. 1993. Corr. 2nd printing 1995; ISBN 978-0387979359. Extract: Google Books |
2016-2023 J. Giesen
updated: 2023, Oct 06